
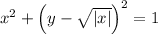
Subtract x² from both sides of the equation.
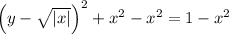
Subtracting x² from itself leaves 0.
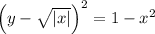
Take the square root of both sides of the equation.
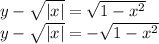
Subtract − √∣x∣ from both sides of the equation.
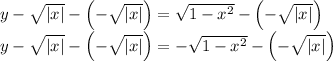
Subtracting − √∣x∣ from itself leaves 0.
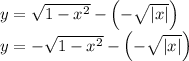
Subtract − √∣x∣from √1- x².
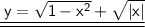
Subtract − √∣x∣from - √1- x².
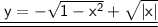
The equation is now solved.
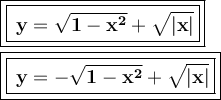
_________________________________
- Refer to the attached image for the graph.