Question

Write an equation of the line below.
-

Answer 1

y = 1/2x - 2

Explanation:

Given points (0, -2) and (8, 2) from the graph:

We can use these values to solve for the slope:

`m = (y2 - y1)/(x2 - x1)`

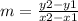
where:

x1 = 0, x2 = 8

y1 = -2, y2 = 2

`m = (y2 - y1)/(x2 - x1) = (2 - (-2))/(8 - 0) = (2 + 2)/(8) = (4)/(8) = (1)/(2)`

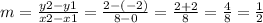
Therefore, our slope is 1/2.

Next, we can determine the value of the y-intercept, which is the the y-coordinate of the point where the graph of the linear equation crosses the y-axis. The y-intercept is also the value of y when x = 0. If you look either at the graph, or one of the points we used to solve for the slope, you'll see that (0, -2) gives us the y-intercept, -2.

Another way to find out the value of the line's y-intercept is to plug in the values of one of the points on the graph into the slope-intercept form y = mx + b:

Let's choose the ordered pair, (8, 2), and our slope, m = 1/2:

y = mx + b

2 =
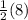`(1)/(2)(8)` + b

2 = 4 + b

Subtract 4 on both sides of the equation to solve for the y-intercept (b):

2 - 4 = 4 + b - 4

-2 = b

It still gives us the same y-intercept value of -2. We can finally put together our linear equation given our slope of 1/2 and y-intercept, -2.

Therefore, our linear equation in slope-intercept form is:

y = 1/2x - 2.