Answer:
m < 1 = 64°
m < 2 = 26°
Explanation:
Given that m < 1 and m < 2 are complementary angles whose sum add up to 90°, and that:
m < 1 = (x + 51)° and m < 2 = 2x°,
We can write the following equation to solve for the measurements of angles 1 and 2:
m < 1 + m < 2 = 90°
Substitute m < 1 and m < 2 into the equation:
(x + 51)° + 2x° = 90°
3x° + 51° = 90°
Subtract 51° on both sides of the equation:
3x° + 51° - 51° = 90° - 51°
3x° = 39°
Divide both sides by 3:
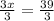
x = 13°
Substite x = 13° into m < 1 and m < 2 to find their measurements:
m < 1 = (x + 51)° = 13° + 51° = 64°
m < 2 = 2x° = 2(13)° = 26°
To check the validity of the answers, we can substitute m < 1 = 64° and m < 2 = 26° into the original equation to see if their measurements add up to 90°:
m < 1 + m < 2 = 90°
64° + 26° = 90°
Therefore, the derived answers are correct.