Question

Use L'Hospital's Rule to find answer

Answer 1

Why do we want to use l'Hopital's Rule in the first place?

If we try to solve as is we get 0/0, which does nothing for us.

l'Hopital's Rule states:

`\lim_(x \to c) (f(x))/(g(x)) = \lim_(x \to c) (f'(x))/(g'(x))`

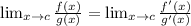
So take the derivative of the top and bottom and then try to solve

`(cos(x) - 2cos(2x))/(1-cos(x))`

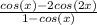
Now take the limit at 0

`(cos(0) - 2cos(2(0)))/(1-cos(0))`

`(1 - 2)/(1 - 1) = (1)/(0)`

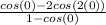
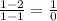
Since 1-cos(0) = 0, we have to look at values of x close to 0 to see what happens with the curve. This is where a graphing calculator comes in handy. But you can put -1 and 1 into the equation to see what it does.

1 - cos(1) and 1 - cos(-1) will give you negative numbers, so the answer is the limit goes to -∞

Explanation: