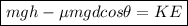Hi there!
We can use the work-energy theorem to solve.
Recall that:
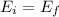
The initial energy equals the final energy (Conservation of Energy). However, we must take into account energy dissipated due to friction in this instance.
The energy lost due to friction is equivalent to the work done by friction. Recall the following:
- Normal force on an incline:

- Force due to friction:
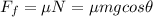
The work due to a force is:
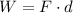
Since the displacement is in the same direction as the force, the dot-product becomes Fd.
The work due to friction then becomes:
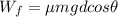
The work due to friction is SUBTRACTED from the initial potential energy.
Initial energy = GPE = mgh
Final energy = KE
Therefore: