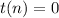Question

NO LINKS!!! Part 2: Complete the sequence​

Answer 1

a) (4, 40) and (5, 80)

b)
`t(n)=2.5 \cdot2^n`

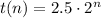
c) see attached

Explanation:

As the value of t(n) doubles each time, we can conclude that this is an exponential function.

Therefore, the missing ordered pairs are (4, 40) and (5, 80)

General form of an exponential function:
`y=ab^x`

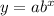
where:

• 
  `a` is the y-intercept (or initial value)
• 
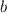  `b` is the base (or growth factor)
• 
  `x` is the independent variable

If
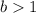`b > 1` then it is an increasing function

If
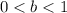`0 < b < 1` then it is a decreasing function

Given:

• (2, 10)
• (3, 20)

Substitute these ordered pairs into the general form of the exponential function:

Equation 1:
`ab^2=10`

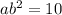
Equation 2:
`ab^3=20`

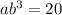
Divide Equation 2 by Equation 1 to find
`b`:

`\implies (ab^3)/(ab^2)=(20)/(10)`

`\implies b=2`

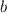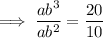
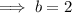
Now substitute the found value of
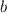`b` into one of the equations and solve for
`a`:

`\implies ab^2=10`

`\implies a\cdot 2^2=10`

`\implies a=(10)/(4)`

`\implies a=2.5`

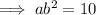
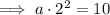
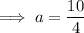
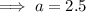
So the final exponential equation is:
`t(n)=2.5 \cdot2^n`

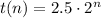
Graphing

Plot the points from the table

To find the y-intercept:

Substitute
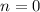`n = 0` into the equation:

`\implies t(0)=2.5 \cdot2^0`

`\implies t(0)=2.5`

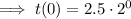
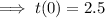
Therefore, the y-intercept is at (0, 2.5)

Asymptote:
`t(n) = 0`

Answer 2

• 40, 80
• t(n) = 5×2^(n-1)
• see attached

Explanation:

The sort of sequence it is can be determined by looking at the differences of n-values and the differences of t(n)-values. When the n-value differences are constant, the nature of the relation between the t(n)-values can tell you the kind of sequence.

a)

Here, the n-values all differ by 1. The t(n)-value differences double with each increase in n. That is, they are 5 and 10. We notice also that the t(n) values double with each increase in n. We can fill the rest of the table using that relationship:

t(n) = t(n-1) × 2 . . . . . each term is double the previous term

t(4) = t(3) × 2 = 20 × 2 = 40

t(5) = t(4) × 2 = 40 × 2 = 80

When the terms of the sequence have a common ratio, the sequence is geometric, and the function describing the sequence is an exponential function.

__

b)

The general term of a geometric sequence is ...

t(n) = t(1) × r^(n-1)

The table tells us the first term is ...

t(1) = 5

And our observation above tells us the common ratio is r = 10/5 = 2. Then the equation of the sequence is ...

t(n) = 5 × 2^(n-1)

__

c)

See the attachment for a graph.