Question

NO LINKS. Part 1: Complete the sequence​

Answer 1

a) (6, 6) and (7, 4)

b)
`t(n)=-2n+18`

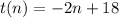
c) see attached

Explanation:

From inspection of the table, we can see that as n increases by 2, t(n) decreases by 4. Therefore, as this a directly proportional relationship, it is a linear function.

So as n increases by 1, t(n) will decrease by 2.

Therefore, the remaining two ordered pairs are:

(6, 6)

(7, 4)

We know that the function decreases by 2 each time n increases by 1, so the slope (gradient) of the linear function will be -2.

Using the point-slope formula:
`y-y_1=m(x-x_1)`

(where
`m` is the slope and
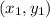`(x_1,y_1)` is a point on the line)

Given:

• 
  `m=-2`
• 
  `(x_1,y_1)=(1,16)`

`\implies y-16=-2(x-1)`

`\implies y=-2x+18`

`\implies t(n)=-2n+18`

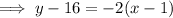
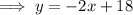
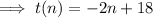
Graphing

To find the y-intercept, substitute
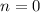`n=0` into the equation:

`\implies t(0)=-2(0)+18=18`

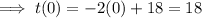
Therefore, the y-intercept is (0, 18)

To find where the line crosses the x-axis, set the equation to zero and solve for n:

`\implies -2n+18=0`

`\implies 2n=18`

`\implies n=9`

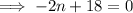
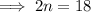
Therefore, the line crosses the x-axis at (9, 0)