The area of quadrilateral DYES is 3.5 square units.
To find the area of quadrilateral DYES, we can break it into two parts: triangle DYE and square DEFG.
1. Area of square DEFG:
Since EFHG is a square and EF = 1, the area of the square is
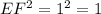 .
.
2. Area of triangle DYE:
The area of a triangle is given by
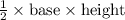 . Here, DE can serve as the base, and AY as the height since triangle DYE is a right-angled triangle with angle DYE being 90 degrees (because DEFG is a square, and thus DE is perpendicular to FG, and extension YG is also perpendicular to DE).
. Here, DE can serve as the base, and AY as the height since triangle DYE is a right-angled triangle with angle DYE being 90 degrees (because DEFG is a square, and thus DE is perpendicular to FG, and extension YG is also perpendicular to DE).
The length of DE is equal to the side of the square DEFG, which is 1. The length of AY is given as 5.
So the area of triangle DYE is:
![\[ \text{Area}_(\triangle DYE) = (1)/(2) * DE * AY = (1)/(2) * 1 * 5 = 2.5 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/middle-school/gqqdbwlr2rgf71xarvgc.png)
3. Area of quadrilateral DYES:
Quadrilateral DYES is composed of the entire square DEFG and triangle DYE.
The area of DYES is therefore:
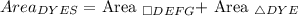
![\[ \text{Area}_(DYES) = 1 + 2.5 = 3.5 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/middle-school/1tb43p3kvjvx4d3nl5fh.png)
So, The answer is 3.5.
The complete question is here:
In the figure below, ABDC, EFHG, and ASHY are all squares; AB=1, EF=1, and AY=5.
What is the area of quadrilateral DYES?