
- If the square of a number is added to 8 times the number, the result is 100. Find x.
Let's take the number as 'x'.
- Square of x = x²
- 8 times x = 8x
We are given that, 8x + x² = 100
Now, let's solve for x.
__________________
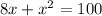
Quadratic equations such as this one can be solved by completing the square. In order to complete the square, the equation must first be in the form x²+bx=c.
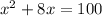
Divide 8, the coefficient of the x term, by 2 to get 4. Then add the square of 4 to both sides of the equation. This step makes the left-hand side of the equation a perfect square.
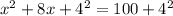
Square 4.
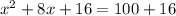
Add 100 to 16.
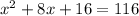
Factor x²+8x+16. In general, when x²+bx+c is a perfect square, it can always be factored as
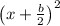 .
.
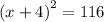
Take the square root of both sides of the equation.

Simplify.
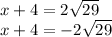
Subtract 4 from both sides of the equation.
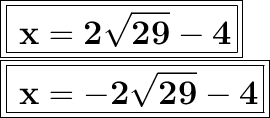
- x can be either of these values.