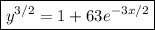Your solution seems fine. What does the rest of the error message say?
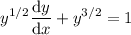
Substitute
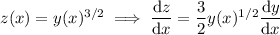
to transform the ODE to a linear one in z :
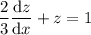
Divide both sides by 2/3 :
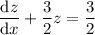
Multiply both sides by the integrating factor,
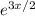 :
:

Condense the left side into the derivative of a product :
![\displaystyle (\mathrm d)/(\mathrm dx)\left[e^(3x/2)z\right] = \frac32 e^(3x/2)](https://img.qammunity.org/2022/formulas/mathematics/college/tftevrrhe58c7t17btr2p6kxjx3rnbl4qx.png)
Integrate both sides and solve for z :
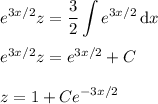
Solve in terms of y :
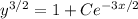
Given that y (0) = 16, we have
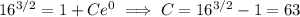
so that the particular solution is