Answer:
2.65 sec , 118.85 feet
Explanation:
Given a parabola in standard form
h(t) = at² + bt + c ( a ≠ 0 )
Then the maximum occurs when
t = -
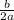
h(t) = - 16t² + 84.8t + 6.49 ← is in standard form
with a = - 16, b = 84.8 , then
t = -
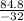= 2.65 seconds
The ball reaches its maximum height at 2.65 seconds
Substitute t = 2.65 into h(t) for maximum height
h(2.65) = - 16(2.65)² + 84.8(2.65) + 6.49
= - 16(7.0255) + 224.72 + 6.49
= - 112.36 + 231.21
= 118.85
The maximum height is 118.85 feet