Question

the first n terms of the progression. The first term and common difference of an arithmetic progression are a and -2. respectively. The sum of the first n terms is equal to the sum of the first 3n terms Express a in terms of n. Hence, show that n = 7 if a = 27.​

Answer 1

If a is the first term of an AP with common difference -2, then the first several terms are

a, a - 2, a - 4, a - 6, a - 8, …

with n-th term a - 2 (n - 1).

The sum of the first n terms is equal to the sum of the first 3n terms :

`\displaystyle \sum_(i=1)^n (a-2(i-1)) = \sum_(i=1)^(3n) (a-2(i-1))`

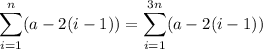
We have

`\displaystyle \sum_(i=1)^N (a-2(i-1)) = (a+2)\sum_(i=1)^N - 2\sum_(i=1)^Ni = (a+2)N - 2\cdot\frac{N(N+1)}2 = (a+1)N-N^2`

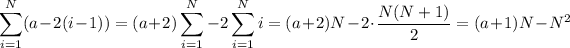
so that in the previous equation, the sums reduce to

`(a+1)n-n^2 = (a+1)(3n)-(3n)^2`

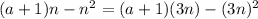
Solve for a :

`(a+1)n-n^2 = (a+1)(3n)-(3n)^2 \\\\ (a+1)n-n^2 = (a+1)(3n)-9n^2 \\\\ 9n^2-n^2 = (a+1)(3n)-(a+1)n \\\\ 8n^2 = (a+1)(2n) \\\\ 4n = a+1 \\\\ \boxed{a=4n-1}`

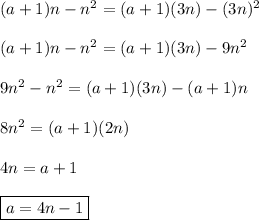
Now if a = 27, we have

27 = 4n - 1

28 = 4n

n = 7

as required.