Answer:
Focus ->
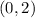
Explanation:
Because the x-term is squared, the parabola must be vertical.
Recall that the equation for a vertical parabola is
 where
where
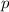 is the distance from the vertex
is the distance from the vertex
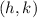 to the focus and
to the focus and
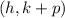 are the coordinates of the focus.
are the coordinates of the focus.
We can tell by the given equation that the vertex must be located at the origin.
Therefore, we can determine the value of
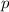 having known the vertex and the direction of the parabola:
having known the vertex and the direction of the parabola:

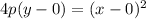
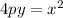
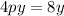
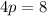
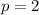
So, given that
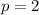 , this means that the coordinates of the focus are
, this means that the coordinates of the focus are
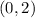 .
.