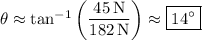Question

Find the resultant force And angle

Answer 1

The first force has magnitude 60 N and makes an angle of -30° relative to the positive horizontal axis (i.e. to the immediate right), while the second force has magnitude 150 N and direction +30° from the horizontal.

In component form, we have

`\vec F_1 = F_(1,x)\,\vec\imath + F_(1,y)\,\vec\jmath \\\\ \vec F_1 = (60\,\mathrm N)\cos(-30^\circ)\,\vec\imath + (60 \,\mathrm N)\sin(-30^\circ)\,\vec\jmath \\\\ \vec F_1 \approx (52.0\,\mathrm N)\,\vec\imath - (30\,\mathrm N)\,\vec\jmath`

`\vec F_2 = F_(2,x)\,\vec\imath + F_(2,y)\,\vec\jmath \\\\ \vec F_2 = (150\,\mathrm N)\cos(30^\circ)\,\vec\imath + (150\,\mathrm N)\sin(30^\circ)\,\vec\jmath \\\\ \vec F_2 \approx (130\,\mathrm N)\,\vec\imath + (75\,\mathrm N)\,\vec\jmath`

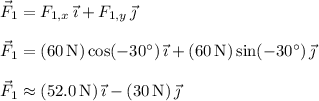
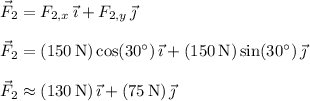
The resultant force is the vector

`\vec F = \vec F_1 + \vec F_2 \\\\ \vec F \approx (182\,\mathrm N)\,\vec\imath + (45\,\mathrm N)\,\vec\jmath`

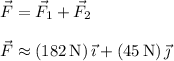
Its magnitude is

`R = \|\vec F\| \\\\ R \approx √((182\,\mathrm N)^2 + (45\,\mathrm N)^2) \\\\ R = 187.35\,\mathrm N \approx \boxed{190\,\mathrm N}`

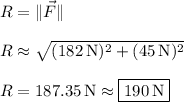
Its direction
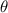`\theta` is such that

`\tan(\theta) \approx (45\,\mathrm N)/(182\,\mathrm N)`

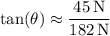
Because the components of the resultant force are both positive, that means the angle
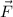`\vec F` makes with the horizontal is between 0° and 90°. So

`\theta \approx \tan^(-1)\left((45\,\mathrm N)/(182\,\mathrm N)\right) \approx \boxed{14^\circ}`