Question

Line 1 passes through points ( 4 , − 4 ) and ( 8 , − 3 ) while line 2 passes through points ( 1 , − 6 ) and ( − 1 , 2 ). Determine whether the lines are parallel, perpendicular, or neither.

Answer 1

`\stackrel{\textit{\Large line 1}}{(\stackrel{x_1}{4}~,~\stackrel{y_1}{-4})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{-3})} ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-3}-\stackrel{y1}{(-4)}}}{\underset{run} {\underset{x_2}{8}-\underset{x_1}{4}}}\implies \cfrac{-3+4}{4}\implies \boxed{\cfrac{1}{4}} \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{\Large line 2}}{(\stackrel{x_1}{1}~,~\stackrel{y_1}{-6})\qquad (\stackrel{x_2}{-1}~,~\stackrel{y_2}{2})} \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{2}-\stackrel{y1}{(-6)}}}{\underset{run} {\underset{x_2}{-1}-\underset{x_1}{1}}}\implies \cfrac{2+6}{-2}\implies \cfrac{8}{-2}\implies \boxed{-4}`

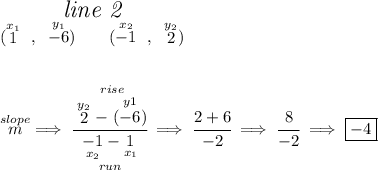
keeping in mind that parallel lines have exactly the same slope, let's check for the slopes hmmm nope, they're not equal, so the lines are not parallel.

keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slopes hmmm

`\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{\cfrac{1}{4}} ~\hfill \stackrel{reciprocal}{\cfrac{4}{1}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{4}{1}\implies -4}}`

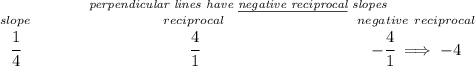
low and behold, Line 2 has a slope that is negative reciprocal to the slope of Line 1, thus, they're indeed perpendicular.