Question

Which expression is equal to

Answer 1

`6i √(3)`

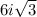
Explanation:

To simplify a negative square root, you can rewrite the
`√(-27)`:

`√(-27)` ==
`√(-1 * 27)`

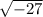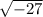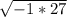
Which can then be rewritten itself as:

`√(-1) * √(27)`

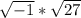
Now, you need to factor the 27, traditionally you will get to remember these but:

`√(3 * 9) * i == \sqrt{3 * 3^(2) }* i`

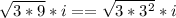
As you are square rooting, the
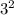`3^(2)` can be cancelled and simplified:

`3 √(3) * i`

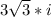
Now, as there is already a 2 before the square root, you can simply multiply the 3i by 2:

`(3i * 2) √(3) = 6i √(3)`

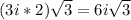
Hope this helps!