You can use the definition:
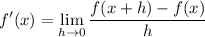
Then if
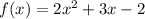
we have

Then the derivative is
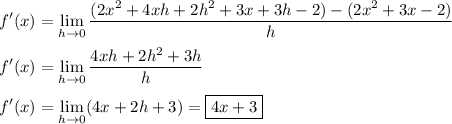
I'm guessing the second part of the question asks you to find the tangent line to f(x) at the point a = 0. The slope of the tangent line to this point is
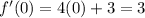
and when a = 0, we have f(a) = f (0) = -2, so the graph of f(x) passes through the point (0, -2).
Use the point-slope formula to get the equation of the tangent line:
y - (-2) = 3 (x - 0)
y + 2 = 3x
y = 3x - 2