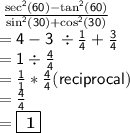Question

Evaluate the following.
(iii) sec² 60° - tan² 60° / sin² 30° + cos² 30°​

Answer 1

`\frac{ {sec}^(2) 60 \: - \: {tan}^(2)60 }{ {sin}^(2)30 + {cos}^(2)30 }`

`{sec}^(2) 60 = {2}^(2) = 4`

`{tan}^(2) 60 = { √(3) }^(2) = 3`

`{sin}^(2) 30 = { ((1)/(2)) }^(2) = (1)/(4)`

`{cos}^(2) 30 = {( ( √(3) )/(2) )}^(2) = (3)/(4)`

`= (4 - 3)/( (1)/(4) + (3)/(4) )`

`(1)/(( (4)/(4) )) = (1)/(1) = 1`

Answer 2

`\huge\boxed{ \bf\:1}`

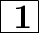
Explanation:

The key element to solve this question is to know the trignometric values of the given angles.

cosec θ, sec θ & cot θ are the reciprocals of sin θ, cos θ & tan θ respectively.

Please refer to the attachment for the trignometric values of 30°, 45° & 60° angles as they are used in the given question.

`\rule{150}{2}`

Now, let's solve this question.

First, let's write the values of the given trignometric degrees.

`\star\sec^(2)(60) = 2^(2)= 4\\ \star\tan^(2)(60) = (√(3) )^(2) = 3\\\star\sin^(2)(30) = ((1)/(2) )^(2) = (1)/(4) \\\star\cos^(2)(30) =( (√(3) )/(2) )^(2) = (3)/(4)`

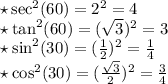
Now, let's solve the given question by substituting the above values & then simplifying by doing the necessary arithmetic operations.

`\sf\:(\sec^(2)(60) - \tan^(2)(60))/(\sin^(2)(30)+\cos^(2)(30))\\\sf\:= 4-3 \: / (1)/(4) + (3)/(4) \\\sf\:= 1 / (4)/(4) \\\sf\:= (1)/(1) * (4)/(4) (reciprocal) \\\sf\:= (4)/(4) \\=\boxed{ \bf\:1}`

`\rule{150}{2}`