✪ Question -:
Herman plans to paint a triangular section of his house. The house is 20 feet long. The height of the triangular section is 8 feet. How many square feet of paint will Herman need?
✪ Explanation -:
Given -
- Base of the house (b = 20 feet)
- Height of the house (h = 8 feet)
Need to find -
- Square feet of paint Herman need to paint the triangular section of the house
Solution -
This question is based on Area of a triangle to solve this question we need to calculate the area of the triangular section of the house.
We know,
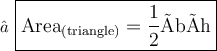
Where,
- h stand for height
- b stand for base
Substituting the value of h = 8 feet and b = 20 feet
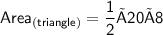
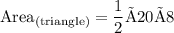
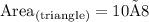

Hence, Herman need 80 square feet of paint to paint the triangular section of his house
![\rule{182mm}{4pt}]()
Additional Information -
Formulas of Area
- Area of a rectangle = Length × Breadth
- Area of a square = side × side
- Area of a circle = π
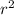
- Area of a parallelogram = Base × Height