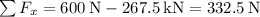Step-by-step explanation:
The net force along the horizontal direction is
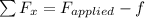
where f is the frictional force. We can find the frictional force by looking at the vertical forces acting on the couch:
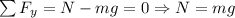
From the definition of frictional force,
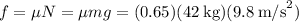
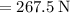
Therefore, the net force on the couch is