Answer :
- Option C (x = 3 or x = -13)
⠀
Explanation :
⠀
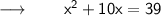
⠀
We can write it as,
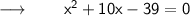
⠀
We have to find the two numbers a and b such that,
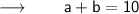
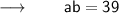
⠀
Obviously, the two numbers are 3 and 13.
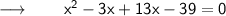
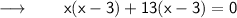
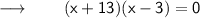
⠀
Whether, the value of x :
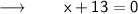
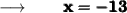
⠀
Whether, the value of x :
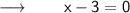

⠀
So,
- Option C (x = 3 or x = -13) is correct.