Question

Mathematical Statistics with Applications Help Homework

Answer 1

7.43: Let
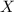`X` denote the random variable for height and
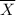`\overline X` for the sample mean. Then if
`\mu` is the mean of

So the probability that the difference between the sample and population means does not exceed 0.5 inch is

`P(|\overline X-\mu|\le0.5) = P\left(\left|(\overline X-\mu)/(0.25)\right|\le(0.5)/(0.25)\right) = P(|Z|\le 2) \approx \boxed{0.95}`

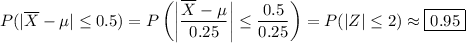
per the empirical or 68/95/99.7 rule.

7.44: For a sample of size n, the sample standard deviation would be
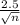`(2.5)/(\sqrt n)`. We want to find n such that

`P(|\overline X-\mu| < 0.4) = 0.95`

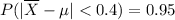
Comparing to the equation from the previous part, this means we would need

`(0.4)/((2.5)/(√(n))) = 0.16\sqrt n = 2 \implies \sqrt n = 12.5 \implies n = 156.25`

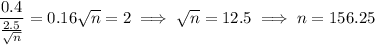
so a sample of at least 157 men would be sufficient.