Answer:
There is only 1 solution for x.
Explanation:
Hi there!


This is a linear-quadratic system. If the line is tangent to the parabola, it means that it would only have 1 solution.
Set y equal:

Move everything to the left side:

Divide both sides by 3:
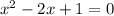
Factor:

Solve for x:
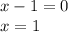
Therefore, the only solution for x when y is set equal for both functions is 1. There is only 1 solution for x, so
 is tangent to the curve
is tangent to the curve
 .
.
I hope this helps!