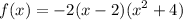Answer:
Explanation:
We want to find a third degree polynomial with zeros x = 2 and x = 2i and f(-1) = 30.
First, note that by the Complex Root Theorem, since x = 2i is a root, x = -2i must also be a root.
Hence, we will have the three factors:
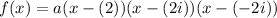
Where a is the leading coefficient.
Expand and simplify the second and third factors:
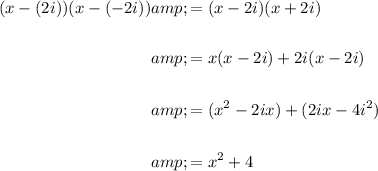
Hence:
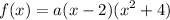
Since f(-1) = 30:
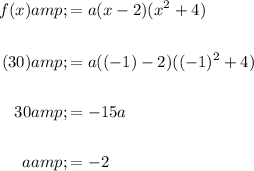
In conclusion, third degree polynomial function is: