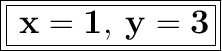
Solve the following using Substitution method
2x – 5y = -13
3x + 4y = 15
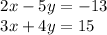
- To solve a pair of equations using substitution, first solve one of the equations for one of the variables. Then substitute the result for that variable in the other equation.
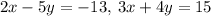
- Choose one of the equations and solve it for x by isolating x on the left-hand side of the equal sign. I'm choosing the 1st equation for now.
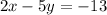
- Add 5y to both sides of the equation.
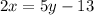
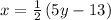
- Multiply
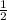 times 5y - 13.
times 5y - 13.

- Substitute
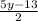 for x in the other equation, 3x + 4y = 15.
for x in the other equation, 3x + 4y = 15.
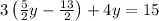
- Multiply 3 times
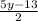 .
.
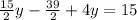
- Add
 to 4y.
to 4y.

- Add
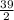 to both sides of the equation.
to both sides of the equation.
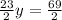
- Divide both sides of the equation by 23/2, which is the same as multiplying both sides by the reciprocal of the fraction.

- Substitute 3 for y in
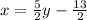 . Because the resulting equation contains only one variable, you can solve for x directly.
. Because the resulting equation contains only one variable, you can solve for x directly.
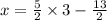

- Add
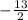 to
to
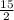 by finding a common denominator and adding the numerators. Then reduce the fraction to its lowest terms if possible.
by finding a common denominator and adding the numerators. Then reduce the fraction to its lowest terms if possible.

- The system is now solved. The value of x & y will be 1 & 3 respectively.