Answer:
Undefined.
Explanation:
We want to find the slope of the graph of the equation:
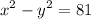
At the point (9, 0).
In other words, we want to evaluate dy/dx when x = 9 and y = 0.
Find dy/dx. We can take the derivative of both sides with respect to x:
![\displaystyle \begin{aligned} (d)/(dx)\left[ x^2 - y^2\right] &= (d)/(dx)\left [ 81\right] \\ \\ 2x - 2y (dy)/(dx) &= 0 \\ \\ (dy)/(dx) &= (x)/(y)\end{aligned}](https://img.qammunity.org/2022/formulas/mathematics/college/crv3js6665t0cp03zye38xhtqccdafbysi.png)
Then the slope of the graph at the point (9, 0) will be:
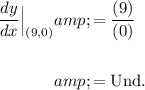
In conclusion, the slope of the graph at the point (9, 0) is undefined.