Answer:

Explanation:
Hi there!
We want to write an equation of the line that is perpendicular to y=3x-1 and passes through (3, -4)
Perpendicular lines have slopes that multiply to get the value of negative one.
Let's first figure out the slope of y=3x-1
The line is written in slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept
3 is in the place of where m is, so 3 is the slope of y=3x-1
Now let's find the slope of the line perpendicular to it.
We can use a formula like this:
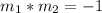
If 3 is
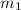 , then:
, then:
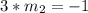
Divide both sides by 3
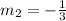
So the slope of the perpendicular line is -1/3
We can write this equation in slope-intercept form. So far, we know that the equation of the line is:
y=
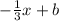
So let's find b
Remember that we are given that the line passes through the point (3, -4). That means that point is a solution to the equation that we're trying to find. Therefore, the values of that point should create a true statement when plugged into the equation.
So we can substitute 3 as x and -4 as y to help solve for b.
-4=

Multiply
-4=
 + b
+ b
Simplify
-4 = -1 + b
Add 1 to both sides to isolate b
-3 = b
Substitute -3 as b in the equation

Hope this helps!