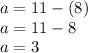Answer:
The numbers are
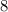 and
and
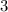 .
.
Explanation:
Let
 and
and
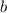 the numbers.
the numbers.
If
 and
and
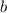 are factors of
are factors of
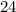 , then
, then
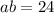
If
 and
and
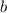 has to add up to
has to add up to
 , the
, the
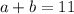
Solving for
 in terms of
in terms of
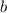 in the equation,
in the equation,
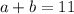 :
:
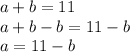
Solving the equation
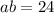 by plugging in
by plugging in
 :
:
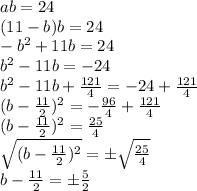
Solving
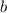 from the positive root:
from the positive root:
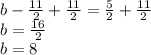
Solving
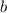 from the negative root:
from the negative root:
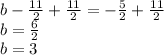
Solving for
 in the equation,
in the equation,
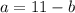 when
when
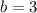 :
:
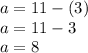
Solving for
 in the equation
in the equation
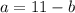 when
when
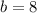 :
: