Answers:
Option 1.) -4|6x + 3| < 16
Option 2.) 8|6x + 3|+ 13 > 5
Option 4.) |4x - 9| ≥ -12
Step-by-step explanation:
All real numbers (R) contain rational and irrational numbers. Therefore, the correct answers are:
Option 1.) -4|6x + 3| < 16
Multiply both sides of the inequality by (-1) to reverse the inequality symbol:
(-1 ) (-4 |6x + 3| ) < 16 (-1 )
4|6x + 3| > - 16
Divide both sides of the inequality by 4:
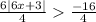
|6x + 3| > - 4 → true for all x values ( – ∞, ∞)
Step-by-step explanation: If the absolute value is greater than a negative number, the solution is all real numbers.
Option 2.) 8|6x + 3|+ 13 > 5
Subtract 13 from both sides of the inequality:
8|6x + 3|+ 13 - 13 > 5 - 13
8|6x + 3| > - 8
Divide both sides of the inequality by 8:

|6x + 3| > - 1 → true for all x values ( – ∞, ∞)
Step-by-step explanation: If the absolute value is greater than a negative number, the solution is all real numbers.
Option 4.) |4x - 9| ≥ -12 → true for all x values ( – ∞, ∞)
Explanation: If the absolute value is greater than or equal to a negative number, the solution is all real numbers. The absolute value of something will always be greater than a negative number.
Example: if x = - 50, then:
|4(-50) - 9| ≥ -12
|-200 - 9| ≥ -12
|-209| ≥ -12
209 ≥ -12 is a true statement. Therefore, x = - 50 is a solution.
If x = 0, then:
|4(0) - 9| ≥ -12
|0 - 9| ≥ -12
|- 9| ≥ -12
9 ≥ -12 is a true statement. Therefore, x = 0 is also a solution.
This proves that regardless of any x values, as long as the inequality is either greater than/ greater than or equal to a negative number, all real numbers are valid solutions for x because the absolute value of something will always be greater than a negative number.