Question

1b. Solve the differential equations

y''+ 4y' + 4y = 0, y(0) = 1 and y'(0) = 1

Note that each equation has right hand side zero. So, you don’t have to use the Laplace transform. You just use the characteristic equaiton.​

Answer 1

No solutions

Explanation:

`y''+4y'+4y=0,\:y(0)=1,\:y'(0)=1\\\\m^2+4m+4=0\\\\(m+2)(m+2)=0\\\\m=-2`

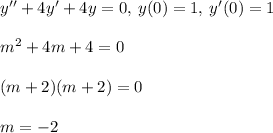
Thus, since we have equal real roots, we use the general solution
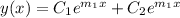`y(x)=C_1e^(m_1x)+C_2e^(m_1x)` and our initial conditions to set up our system of equations:

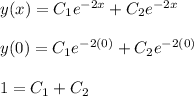`y(x)=C_1e^(-2x)+C_2e^(-2x)\\\\y(0)=C_1e^(-2(0))+C_2e^(-2(0))\\\\1=C_1+C_2` <-- First one

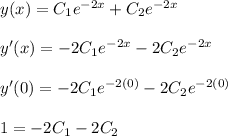`y(x)=C_1e^(-2x)+C_2e^(-2x)\\\\y'(x)=-2C_1e^(-2x)-2C_2e^(-2x)\\\\y'(0)=-2C_1e^(-2(0))-2C_2e^(-2(0))\\\\1=-2C_1-2C_2` <-- Second one

Solve the system

`C_1+C_2=-2C_1-2C_2\\\\3C_1+3C_2=0\\\\3C_1=-3C_2\\\\C_1=-C_2`

`1=C_1+C_2\\\\1=-C_2+C_2\\\\1=0`

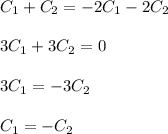
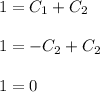
Therefore, there are no solutions to the differential equation given the initial conditions.