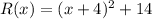Question

Convert R(x) to vertex form.

R(x)=x²+8x +30

Answer 1

R(x) = (x + 4)² + 14

Explanation:

The equation in vertex form is

a(x - h)² + k

Use the method of completing the square

add/ subtract ( half the coefficient of the x- term)² to x² + 8x

R(x) = x² + 8x + 30

= x² + 2(4)x + 16 - 16 + 30

= (x + 4)² + 14 ← in vertex form

Answer 2

`R(x) = (x + 4)^(2) + 14`

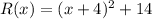
Explanation:

Given the quadratic function:
`R(x) = x^(2) + 8x + 30`

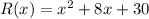
where a = 1, b = 8, and c = 30

Since a > 0, then the parabola is facing upward, and its vertex is the minimum point in the graph. We can determine the vertex (h, k ) through the x and y coordinates of the axis of symmetry:

`x = (-b)/(2a) = (-8)/(2(1)) = -4`

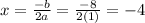
Now that we have the value of x coordinate (or h), plug this value into the quadratic function to solve for the value of the y-coordinate ( k ):

`R(x) = (-4)^(2) + 8(-4) + 30 = 15 -32 + 30 = 14`

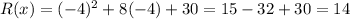
Therefore, the vertex of the quadractic function is given by (-4, 14).

Now that we have the value of the vertex, we can rewrite the quadratic function into its vertex form:

`R(x) = (x - (-4)^(2) + 14`

`R(x) = (x + 4)^(2) + 14`