Question

Find all the zeros of the equation y=x^4+3x^3+x^2-12x-20

Answer 1

`x=2, x=-2`;
`(-3\pm i√(11))/(2) \in \mathbb{C}`

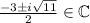
Step-by-step explanation:

Zeroes are found by setting the RHS = 0.

Since the quantity
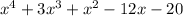`x^4+3x^3+x^2-12x-20` is a 4th degree polynomial there isn't a formula that gives us the solution, so we're stuck having to divide: to do so we make THE LIST: you list the divisors of the constant term without its sign (20: 1,2,4,5,10,20), the divisor of the lead coefficient (1), and you divide the first by the second in any possible way, adding a plus or minus:

`\pm1, \pm2, \pm4, \pm5,\pm10,\pm20`. At this point you just have to check, replacing each one in the equation until you find two values that work (why two? You need to lower the degree of the polynomial by two, if you found only one you'd be stuck with a third degree equation which doesn't have an "easy" solving formula).

After some adding and multiplying you find that both 2 and -2 make the expression to zero. At this point you have two options

First is to divide the given expression by
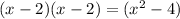`(x-2)(x-2)=(x^2-4)` or, as I did in the image, notice that you will end up with a 2nd degree polynomial, whose coefficient you find by multiplying and confronting with the original equation.

Either way, you will end up with

`(x+2)(x-2)(x^2+3x+5)=0`

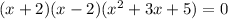
First two factors will give
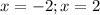`x=-2; x=2` respectively, while the third term has no real solutions (it still offers a pair of solutions in
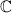`\mathbb{C}` which I'll add for the sake of completeness, but you're most likely required to look for real solutions only).

Answer 2

x = 2, -2

Step-by-step explanation:

`\sf y=x^4+3x^3+x^2-12x-20`

Find a factor for this equation:

-5 < x < 5

-------------

f(-3) = 25

f(-2) = 0

f(-1) = -9

f(0) = -20

f(1) = -27

f(2) = 0

f(3) = 115

Hence found that ( x -2) and ( x + 2) are the factor of the following equation.

Divide both by the following equation:

`\sf \rightarrow (x^4+3x^3+x^2-12x-20)/(\left(x-2\right)\left(x+2\right))`

`\sf \rightarrow (\left(x-2\right)\left(x+2\right)\left(x^2+3x+5\right))/(\left(x-2\right)\left(x+2\right))`

`\sf \rightarrow x^2+3x+5`

Using quadratic formula:
`\sf x = ( -b \pm √(b^2 - 4ac))/(2a) \ \ when \ \ ax^2 + bx + c = 0`

`\sf \hookrightarrow x_(1,\:2)=(-3\pm √(3^2-4\cdot \:1\cdot \:5))/(2\cdot \:1)`

`\hookrightarrow x=-(3)/(2)+i(√(11))/(2),\:x=-(3)/(2)-i(√(11))/(2)`

Thus the zero's of the function are:

x = 2, -2