Answer:
Given equation:
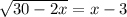
Square both sides:
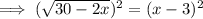

Expand the right side:

Add
 to both sides:
to both sides:
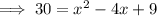
Subtract 30 from both sides:
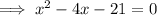
Factor:
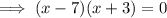
Therefore,
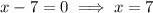

Substitute both values of
 into the original equation to check:
into the original equation to check:
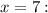
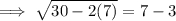
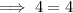
correct!

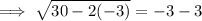
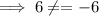
incorrect!
Therefore,
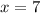 is the only correct solution, and
is the only correct solution, and
 is the extraneous solution
is the extraneous solution
**Extraneous solution: a root of a transformed equation that is not a root of the original equation**