Solving for a Function given its derivative and a point
Answer:

Explanation:
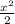 is just the the derivative of
is just the the derivative of
 since it it is the slope of the line tangent to the curve at
since it it is the slope of the line tangent to the curve at
 . To find how
. To find how
 is defined, we'll just take the anti-derivative of
is defined, we'll just take the anti-derivative of
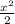 .
.
Recall:
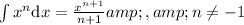
Solving for
 :
:
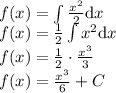
We still have to solve for
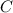 . Note that the point
. Note that the point
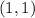 has to be on our graph so
has to be on our graph so
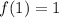 or
or
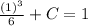 .
.
Solving for
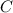 :
:
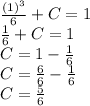
We can finally write
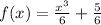 or
or
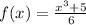 . Since
. Since
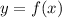 , we can write it as
, we can write it as
 as well.
as well.