Answer:
A)360
B)180
Explanation:
Part-A:
For this question, we don't have to care about what integer they are, we just need to care about the number of integers we are given. considering the question, we understand that we are dealing with permutation .we're given 6 numbers so we want to figure out the permutation of 4 out of 6. the formula which is used for permutation is given by,

where:
- n refers to total number of objects
- r means the number of objects selected
we've already sorted out that
substitute:
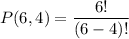
simplify parentheses:

simplify division:
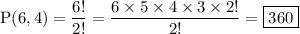
hence,
360 plates of vehicles consisting of 4 different digits can be made out of the integer 4,5,6,7,8,9
Part-B:
to solve this question, we need to know about the divisibility rule of 2 which is A number is divisible by 2 if the last digit is an even number
notice that half the values of the set are even, thus half of our total permutations will be even and thus divisible by 2, since we have already figured out the permutations of 4 digits plate out of 6 i.e 360 therefore 180 of these number will be divisible by 2
Alternate:
[copyright:All credits go to corsaqix ]
so it is a four digit plate. After we choose the last digit, we only need 3 digits, choosing from 5 values left. The answer can be therefore be found by multiplying of possible values for the last digit (3) by the number of ways re-arrange 3 distinct values (3!) by the number of ways to choose 3 values from 5, giving the same answer of 3 x 3! x C(5,3) = 180.