Solving for coordinates of the endpoint given the midpoint and the other endpoint
Answer:
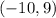
Explanation:
Recall that if you have the two points,
 and
and
 , the midpoint between them is
, the midpoint between them is
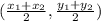 .
.
We let
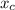 be the
be the
 -coordinate of point
-coordinate of point
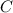 and
and
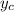 for the
for the
 -coordinate of point
-coordinate of point
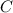 .
.
The problem tells us that point
 is the midpoint of
is the midpoint of
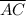 . This means that the point
. This means that the point
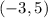 is the same point as
is the same point as
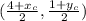 .
.
Solving for
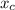 :
:
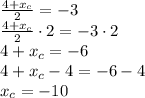
Solving for
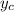 :
:

The coordinates of point
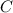 is
is
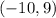 .
.