Question

A line is perpendicular to y = -1/5x+1

and intersects the point (-5,1).
What is the equation of this
perpendicularline?
y = [?]x+ [
Hint: Use the Point-Slope Form: y - y1 = m(x – X1)
Then write the equation in slope-intercept form.

Answer 1

`y = 5\, x + 26`.

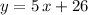Explanation:

Start by finding the slope of the line perpendicular to
`y = (-1/5)\, x + 1`.

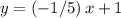The slope of
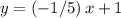`y = (-1/5)\, x + 1` is
`(-1/5)`.

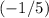In a plane, if two lines are perpendicular to one another, the product of their slopes would be
`(-1)`.

Let
`m` denote the slope of the line perpendicular to
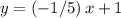`y = (-1/5)\, x + 1`. The expression
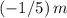`(-1/5)\, m` would denote the product of the slopes of these two lines.

Since these two lines are perpendicular to one another,
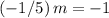`(-1/5)\, m = -1`. Solve for
`m`:
`m = 5`.

The
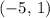`(-5,\, 1)` is a point on the requested line. (That is,
`x_(1) = -5` and
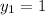`y_(1) = 1`.) The slope of that line is found to be
`m = 5`. The equation of that line in the point-slope form would be:

`y - 1 = 5\, (x - (-5))`.

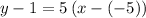Rewrite this point-slope form equation into the slope-intercept form:

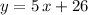`y = 5\, x + 26`.