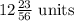The calcuuated length of the segment AC is
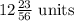
How to determine the length of the segment AC
From the question, we have the following parameters that can be used in our computation:
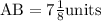
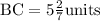
Using the above as a guide, we have the following:
AC = AB + BC
Substitute the known values into the equation
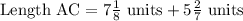
Evaluate the sum of the integers
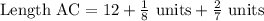
Take the LCM and add the fractions
This gives
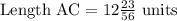
Hence, the length of the segment AC is