Starting with the general
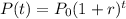 and being told
and being told
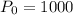 and
and
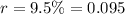 , we have the function
, we have the function
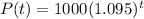
Now, for the population to double, we need to figure out what
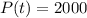 :
:
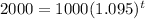
To solve this, first divide by 1000, to isolate the exponential portion:
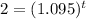
At this point, you have a few options, but they'll all come down to some logarithm. Your choice is what base log you use. The typical ones are base
 (AKA the natural log) or base 10 (AKA the common log). But you could also use any base.
(AKA the natural log) or base 10 (AKA the common log). But you could also use any base.
I'll go at this with the natural log, but you can replace that with any other base log. So, first you'll take the natural log of both side:
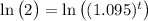
The reason for this is that the exponent inside that natural log on the right side gets to come down using one of the rules of logarithms.
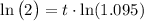
To finish that, you just divide both sides by ln(1.095):
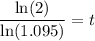
Throw that into a calculator, do a little rounding, and you've got your answer.
Side note: You might have noticed that our first step was to divide out the original population. So it didn't really matter if you started with 1000 people or 10000000 people. The doubling time for an exponential function only depends on the growth rate.