Question

Find an equation of the line passing through the pair of points. Write the equation in the form Ax +By = C.

(-7,2), (-8,-3)

Answer 1

9514 1404 393

Answer:

5x -y = -37

Explanation:

One way to find the coefficients A and B is to use the differences of the x- and y-coordinates:

A = Δy = y2 -y1 = 2 -(-3) = 5

B = -Δx = -(x2 -x1) = -(-7 -(-8)) = -1

Then the constant C can be found using either point.

5x -y = 5(-7) -2 = -37

The equation of the line is ...

5x -y = -37

_____

Additional comment

This approach comes from the fact that the slope of a line is the same everywhere.

`(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)=(\Delta y)/(\Delta x)\\\\\Delta x(y-y_1)=\Delta y(x-x_1)\qquad\text{cross multiply}\\\\\Delta y(x-x_1)-\Delta x(y-y_1)=0\qquad\text{subtract y term}\\\\\Delta y(x) -\Delta x(y) = \Delta y(x_1)-\Delta x(y_1)\qquad\text{Ax+By=C form}`

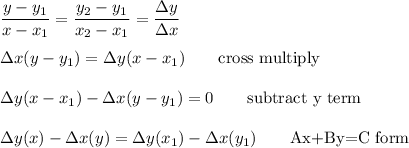
The "standard form" requires that A be positive, so we chose point 1 and point 2 to make sure that was the case.