Answer:
see explanation
Explanation:
Using the identities
1 + cot²x = cosec²x
cosec²x =
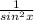 , cotx =
, cotx =

Consider the left side
cos²A + cos²A cot²A ← factor out cos²A from each term
= cos²A(1 + cot²A)
= cos²A × cosec²A
= cos²A ×
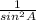
=
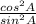
= cot²A
= right side , thus proven