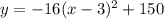Answer:
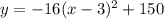
Explanation:
Given the points (3, 150) and (1, 86):
And since the parabola is facing down, then the vertex (h, k) is the maximum point of the parabola, which is given by the ordered pair, (3, 150).
Thus, we can plug those h and k values into the following equation in vertex form:
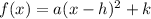
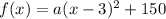
Next, we can use the x and y values of the other ordered pair, (1, 86), and plug those into the equation:
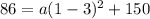
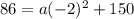
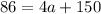
We must now subtract 150 from both sides of the equation:
86 - 150 = 4a + 150 - 150
-64 = 4a
Now we can solve for the value of a :
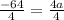
-16 = a
Therefore, the equation of the parabola in vertex form is: