Question

I believe the theorem is the Intermediate Value Theorem.

Answer 1

Yes you have the correct theorem.

The idea is to get everything to one side so we can form a function

`\sin\left(e^(2x)\right) = 2x-1\\\\\sin\left(e^(2x)\right)-2x+1 = 0\\\\f(x) = \sin\left(e^(2x)\right)-2x+1\\\\`

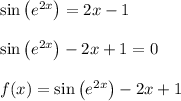
Afterward, we plug in x = 0 to find that

`f(x) = \sin\left(e^(2x)\right)-2x+1\\\\f(0) = \sin\left(e^(2*0)\right)-2*0+1\\\\f(0) = \sin\left(1\right)+1\\\\f(0) \approx 1.84147\\\\`

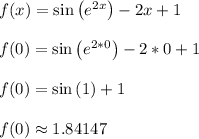
I set my calculator to radian mode, which is fairly common in many calculus courses.

Repeat for x = 1

`f(x) = \sin\left(e^(2x)\right)-2x+1\\\\f(1) = \sin\left(e^(2*1)\right)-2*1+1\\\\f(1) \approx -0.10615\\\\`

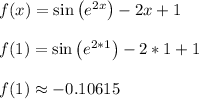
We see that f(x) changes in sign from positive to negative, when going from x = 0 to x = 1. Because f(x) is continuous, there must be at least one point in the road where it cuts through the x axis when f(x) = 0. This is the place where the intermediate value theorem kicks in.

Therefore, f(x) has at least one root on the interval 0 < x < 1. We don't know what the solutions are, or how many. We only know that at least one exists on this interval.

All of those ideas then extend back to the original equation. Since f(x) has at least one root, this must mean the original equation has at least one solution.