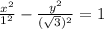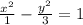1 Answer

Siefix · Answer 1 · 2023-08-25T08:49:18+0000

Explanation:

Use these equations.

Equation of a Hyperbola, centered at orgin

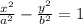
$\frac{ {x}^(2) }{ {a}^(2) } - \frac{ {y}^(2) }{ {b}^(2) } = 1$

where a is the major axis

B is the minor axis.

Since a and X are first, the x axis is the major.

This also means the x axis contains the vertices and foci as well.

The equation of vertices when x is major axis is

(x ±a)

Since the vertices are (±1,0), and the orgin is (0,0). The length of a is 1.

So a=1.

The equation of foci is

(x±c)

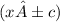
Where c is formed by

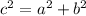
${c}^(2) = {a}^(2) + {b}^(2)$

We know that c is 2 since the distance from the foci and center is 2. A is 1, so let find b.

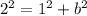
${2}^(2) = {1}^(2) + {b}^(2)$

$4 = 1 + {b}^(2)$

$3 = {b}^(2)$

√(3) = {b}

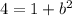
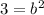
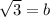
So our equation is

$\frac{ {x}^(2) }{1 {}^(2) } - \frac{ {y}^(2) }{ (√(3)) {}^(2) } = 1$

$\frac{ {x}^(2) }{1} - \frac{ {y}^(2) }{3} = 1$

Please log in or register to add a comment.