Question

For the following true conditional statement, write the converse. If the converse is also true, combine the statements as a biconditional.

If x = 7, then x2 = 49.

A. If x2 = 49, then x = 7. False
B. If x2 = 49, then x = 7. True; x = 7 if and only if x2 = 49.
C. If x = 7, then x2 = 49. True; x = 7 if and only if x2 = 49.
D. If x2 = 49, then x = 7. True; x2 = 49 if and only if x = 7.

Answer 1

Answer: Choice A

If x^2 = 49, then x = 7. False.

===========================================================

Step-by-step explanation:

The template for any conditional expression is "If P, then Q". The P and Q are placeholders for any logical statement.

In this case, P holds the place of "x = 7" and Q holds the place of "x^2 = 49"

When forming the converse, we simply swap the locations of P and Q.

The converse of "If P, then Q" is "If Q, then P".

So If x^2 = 49, then x = 7 will be part of the answer. The order is important.

As you can probably guess, this converse is false because there's the possibility that x = -7 which isn't mentioned. Note that x^2 = (-7)^2 = 49 to show that x = -7 is a solution to x^2 = 49.

In other words, if x^2 = 49, then x = 7 or x = -7. We can shorten this to saying
`x = \pm 7`

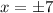
So this is why choice A is the final answer.