Solve for x
2x - 5y = 1
We need to group all the variable terms on one side and all the constant terms on the other side of the equation. Therefore move the term -5y to the other side of equation.
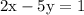
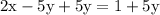
Subtract -5y from both sides of the equation
Simplify 2x - 5y + 5y = 1 + 5y
Cancel -5y with 5y
Reorder 1 + 5y so highest order terms are first
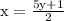
Move factors not having X from the left side of equation 2x = 5y + 1
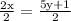
Divide both sides of equation 2x = 5y + 1 by 2
Cancel 2 with 2
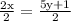
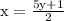
Therefore, the x of 2x - 5y = 1 is
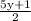
Solve for y
2x - 5y = 1
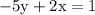
Reorder 2x -5y so highest order terms are first
-5y = -2x + 1
We need to group all the variable terms on one side and all the constant terms on the other side of the equation. Therefore move the term 2x to the other side of equation -5y + 2x = 1
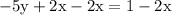
Subtract 2x from both sides of the equation
Simply - 5y + 2x -2x = 1 - 2x
Cancel 2x with -2x
Reorder 1 - 2x so highest order terms are first
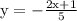
Move factors not having y from the left side of equation -5y = -2x + 1
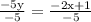
Divide both sides of equation -5y = -2x +1 by -5
Simplify
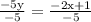
Cancel 5 with -5
Resolve sign on fraction
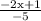
Therefore, the y of 2x-5y = 1 is
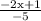
Solve for x
3x + 2y = 11
We need to group all the variable terms on one side and all the constant terms on the other side of the equation. Therefore move the term 2:y to the other side of equation 3 x + 2y - 2y = 11 - 2y
Subtract 2y from the both sides of the equation
Simplify 3x + 2y - 2y = 11 - 2y
Cancel 2y with 2y
Reorder 11 - 2y so highest order terms are first
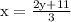
Move the factors not having x from the left side of equation 3x = -2y +11
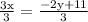
Divide both sides of equation 3x = 2y + 11 by 3
Cancel 3 with 3
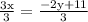
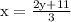
Therefore, the x for 3x + 2y = 11 is

Solve for y
2y + 3x = 11
Reorder 3x + 2y so highest order terms are first

We need to group all the variable terms on one side and all the constant terms on the other side of the equation. Therefore move the term 2:y to the other side of equation 2y + 3x = 11
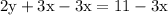
Subtract 3y from the both sides of the equation
Simplify 2y + 3x - 3x = 11 - 3x
Cancel 3x with - 3x
Reorder 11 - 3x so highest order terms are first
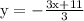
Move factors not having y from the left side of equation 2y = -3x + 11
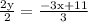
Divide both sides of equation 2y = -3x + 11 by 2
Cancel 2 with 2

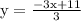
Therefore, the y for 2y + 3x = 11 is
