Question

A satellite is to be launched into an orbit of radius,r Show that v = 2gr, where V is the

launch speed

Answer 1

Step-by-step explanation:

We start by using the conservation law of energy:

`\Delta{K} + \Delta{U} = 0`

or

`(1)/(2)mv^2 - G(mM)/(r) = 0`

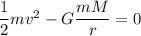
Simplifying the above equation, we get

`v^2 = 2G(M)/(r)`

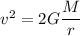
We can rewrite this as

`v^2 = 2\left(G(M)/(r^2)\right)r`

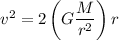
Note that the expression inside the parenthesis is simply the acceleration due to gravity
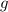`g` so we can write

`v^2 = 2gr`

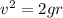
where
`v` is the launch velocity.