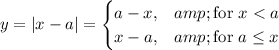Question

Rewrite the equation without absolute value.
y=|x-3|+|x-2|-|x-5|

Answer 1

y = {-x, x < 2; x-4, 2 ≤ x < 3; 3x -10, 3 ≤ x < 5; x, 5 ≤ x}

Explanation:

The absolute value function is a piecewise linear function that changes its definition when its argument changes sign.

Here, the three different absolute value expressions will change their behavior at three different values of x. That is, this equation will be described by a piecewise linear function in four (4) pieces.

For x < 2:

y = (3 -x) +(2 -x) -(5 -x) = -x

For 2 ≤ x < 3:

y = (3 -x) +(x -2) -(5 -x) = x -4

For 3 ≤ x < 5:

y = (x -3) +(x -2) -(5 -x) = 3x -10

For 5 ≤ x:

y = (x -3) +(x -2) -(x -5) = x

In summary, the equation can be written ...

`y=\begin{cases}-x,&\text{for }x < 2\\x-4,&\text{for }2\le x < 3\\3x-10,&\text{for }3\le x < 5\\x,&\text{for }5\le x\end{cases}`

_____

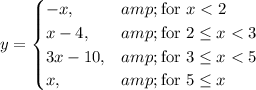
Additional comment

The absolute value function itself can be described by ...

`y=|x-a|=\begin{cases}a-x,&\text{for }x < a\\x-a,&\text{for }a\le x\end{cases}`