Question

What is 5 to the power of 3 divided by 5 to the power of 6?

Answer 1

1/5³ = 1/125 = 5⁻³

Explanation:

It can be useful to remember that an exponent signifies repeated multiplication.

5^3 = 5×5×5

5^6 = 5×5×5×5×5×5

Then the ratio is ...

`(5^3)/(5^6)=(5*5*5)/(5*5*5*5*5*5)=(1)/(5*5*5)=\boxed{(1)/(125)}`

__

If you want to leave this in terms of exponents, you can see that factors in the denominator cancel (subtract from) those in the numerator. That is ...

`(5^3)/(5^6)=(5^(3-3))/(5^(6-3))=(5^0)/(5^3)=\boxed{(1)/(5^3)}`

The same sort of exponent arithmetic works to leave a numerator value with a negative exponent:

`(5^3)/(5^6)=(5^(3-6))/(5^(6-6))=(5^(-3))/(5^0)=(5^(-3))/(1)=\boxed{5^(-3)}`

_____

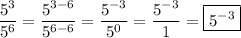
Additional comment

These ideas are formulated as the rules of exponents:

• (a^b)/(a^c) = a^(b-c)
• 1/(a^b) = a^-b