Answer:
If the point
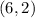 does satisfy the equation,
does satisfy the equation,
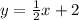 , the point is on the line. Otherwise it's not.
, the point is on the line. Otherwise it's not.
Explanation:
Points that are on the line actually satisfy the equations of their respective lines. If the point
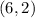 does satisfy the equation,
does satisfy the equation,
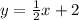 , the point is on the line. Otherwise it's not.
, the point is on the line. Otherwise it's not.
Testing if
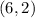 is on the line,
is on the line,
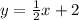 :
:
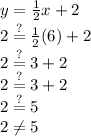
The point
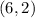 does not satisfy the equation,
does not satisfy the equation,
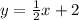 , so the point is not on the line.
, so the point is not on the line.